Minmax Search vs. Alpha-Beta Pruning: Choosing the Best for Game AI
Table of Contents
Introduction
When creating AI for strategic games, the Minmax algorithm is a fundamental tool for making decisions in two-player games with opposing objectives. However, the complexity of such games often leads to computational challenges, which can be mitigated with Alpha-Beta Pruning. This technique optimizes the Minmax algorithm by reducing the number of nodes that need to be explored, allowing for more efficient decision-making.
In this blog post, we will explore the Minmax algorithm using Alpha-Beta Pruning with an example from Connect Four, and walk through a Python implementation.
This article will provide a detailed comparison between the Minmax Search algorithm and Alpha-Beta Pruning, helping you understand the scenarios where each is most effective. Whether you’re developing for chess, Connect Four, or other strategic games, this guide will help you decide on the best approach for your game AI.
What is the Minmax Algorithm?
The Minmax algorithm is a decision rule used for minimizing the possible loss in a worst-case scenario. In games, it helps the AI to choose the move that maximizes its chances of winning while minimizing the opponent’s chances. The algorithm assumes that both players play optimally.
Understanding Connect Four
Connect Four is a two-player strategy game where players take turns dropping colored discs into a vertical grid. The objective is to connect four discs vertically, horizontally, or diagonally. The first player to do so wins the game. The challenge for AI in Connect Four is to choose the optimal move at each turn, considering both immediate opportunities and future possibilities.
The Minmax algorithm will:
- Generate the game tree down to a specified depth (due to the large number of possible moves).
- Evaluate the utility of each terminal node based on how favorable the board is to the current player.
- Propagate the utility values back up the tree to determine the best move.
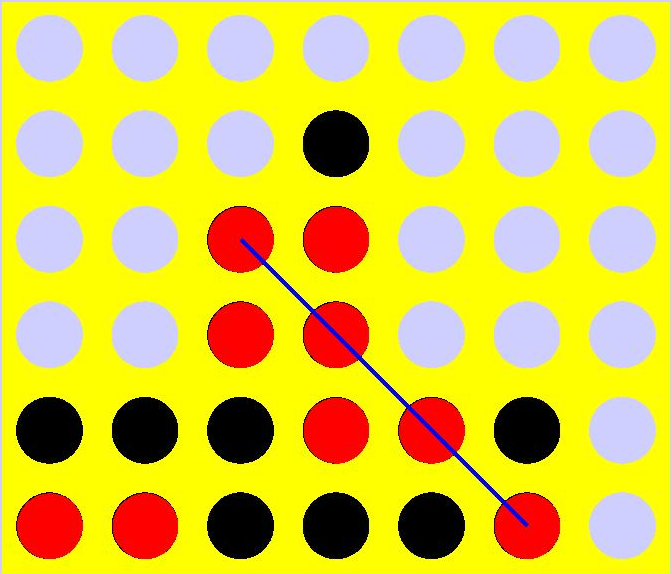
The Minmax Algorithm Explained
The Minmax algorithm is used to make decisions in games by simulating all possible moves up to a certain depth, evaluating the outcome of each move, and then selecting the move that maximizes the AI’s chances of winning while minimizing the opponent’s chances.
Step-by-Step Breakdown in Connect Four
Why Alpha-Beta Pruning?
Minmax, though effective, can be computationally expensive as it explores every possible move. In larger games like chess, the number of possible states (nodes in the tree) grows exponentially. Alpha-Beta Pruning addresses this by “pruning” branches that cannot possibly influence the final decision, thereby reducing the number of nodes that need to be evaluated.
How It Works
Alpha-Beta Pruning keeps track of two values:
- Alpha: The best value that the maximizer can guarantee.
- Beta: The best value that the minimizer can guarantee.
During the tree traversal, if the minimizer’s node value is less than or equal to alpha (α ≥ β), further exploration of that node is unnecessary as the maximizer will never choose that path. This significantly reduces the number of nodes evaluated.
Understanding the Alpha-Beta Process
The AI must decide its next move. The algorithm will evaluate each possible move by simulating all outcomes, pruning branches where the minimizer’s (opponent’s) best response is worse than a previously considered branch.
- Initial Alpha-Beta Values: Alpha is set to negative infinity, and Beta is set to positive infinity.
- Exploring Moves: The AI checks each possible move, calculating the Minmax value for each, updating Alpha and Beta as it goes.
- Pruning: If a move results in a Beta value that’s less than or equal to Alpha, the AI stops exploring that branch.
Implementing Minmax with Alpha-Beta Pruning in Connect Four
Let’s implement the Minmax algorithm with Alpha-Beta Pruning in Python, specifically tailored for Connect Four.
def minmax(board, depth, is_maximizing, alpha, beta):
if depth == 0 or is_terminal_node(board):
return evaluate_board(board)
if is_maximizing:
max_eval = float('-inf')
for col in get_valid_locations(board):
row = get_next_open_row(board, col)
temp_board = board.copy()
drop_piece(temp_board, row, col, 1) # 1 represents AI's piece
eval = minmax(temp_board, depth - 1, False, alpha, beta)
max_eval = max(max_eval, eval)
alpha = max(alpha, eval)
if beta <= alpha:
break # Beta cut-off
return max_eval
else:
min_eval = float('inf')
for col in get_valid_locations(board):
row = get_next_open_row(board, col)
temp_board = board.copy()
drop_piece(temp_board, row, col, 2) # 2 represents opponent's piece
eval = minmax(temp_board, depth - 1, True, alpha, beta)
min_eval = min(min_eval, eval)
beta = min(beta, eval)
if beta <= alpha:
break # Alpha cut-off
return min_evalDetailed Example: AI’s Turn in Connect Four
Let’s consider a situation in Connect Four where the AI needs to make a move. The current board looks like this:
0 1 2 3 4 5 6
0 . . . . . . .
1 . . . . . . .
2 . . . O . . .
3 . . X O . . .
4 . X O X . . .
5 X O X O . . .The AI (playing as 'X') needs to decide its next move.
Step 1: Generate the Game Tree
The algorithm simulates each possible move by placing an ‘X’ in any of the columns that are not full. For each of these potential moves, it generates new board states and continues this process until the depth limit is reached or the game ends.
Step 2: Evaluate Terminal Nodes
At the terminal nodes (where the depth limit is reached or the game ends), the board is evaluated:
- A winning move for ‘X’ might be assigned a value of +100.
- A winning move for ‘O’ might be assigned a value of -100.
- A draw could be valued at 0.
Step 3: Backpropagate Values
The algorithm then backpropagates these values through the tree. If it’s the AI’s turn (maximizing player), it picks the highest value among its possible moves. If it’s the opponent’s turn (minimizing player), it picks the lowest value.
Step 4: Pruning with Alpha-Beta
As the algorithm evaluates different branches, it uses Alpha and Beta values to prune branches that won’t be selected. For example, if placing an ‘X’ in column 3 is better than placing it in column 2, the algorithm might not fully evaluate all outcomes for column 2 if it’s already clear that column 3 is the superior choice.
Performance Analysis
The performance improvement brought by Alpha-Beta Pruning can be significant. Without pruning, the algorithm might explore \(O(b^d)\) nodes, where b is the branching factor and d is the depth of the tree. With Alpha-Beta Pruning, the effective branching factor can be reduced, making it feasible to search deeper in the tree.
Here’s a diagram that illustrates the performance comparison of the Minmax algorithm with and without Alpha-Beta Pruning. The diagram visually represents the execution outcome of our program, highlighting the difference in nodes evaluated and time taken at different search depths,
And here are the statistics from the program above, with and without Alpha-Beta Pruning, at different search depths in Connect Four,
Key Observations
| Model | Nodes Evaluated (With Pruning) | Time Taken (With Pruning) | Nodes Evaluated (Without Pruning) | Time Taken (Without Pruning) |
|---|---|---|---|---|
| 2 | 13 | 2.44 ms | 49 | 4.16 ms |
| 4 | 97 | 13.46 ms | 2,401 | 268.43 ms |
| 6 | 685 | 134.01 ms | 117,649 | 11,276.61 ms |
- Nodes Evaluated: With Alpha-Beta Pruning, the number of nodes evaluated is significantly lower than without pruning. At a depth of 6, the pruning algorithm evaluates only 685 nodes compared to 117,649 nodes without pruning.
- Time Taken: The time taken to evaluate nodes with Alpha-Beta Pruning is drastically reduced. For instance, at depth 6, the pruned algorithm takes about 134 milliseconds, whereas the unpruned algorithm takes over 11,276 milliseconds.
Use Cases
When to Choose Minmax Search
- Small-scale games with limited branching factors
- Scenarios where optimal, exhaustive search is necessary
- Applications with high computational resources
When to Choose Alpha-Beta Pruning
- Large, complex games with numerous possible moves
- Applications requiring faster AI decision-making
- Situations with limited computational resources
Yugensys as an Alternative
Yugensys offers customizable AI solutions that adapt the principles of Minmax Search and Alpha-Beta Pruning based on specific game requirements. By tailoring decision-making algorithms to the complexity of the game, Yugensys provides efficient and optimized performance across various game genres. With extensive expertise in AI and machine learning, Yugensys enables developers to incorporate advanced decision-making without the high computational cost associated with traditional methods.
Conclusion
The combination of the Minmax algorithm and Alpha-Beta Pruning is crucial for developing AI that can efficiently and effectively play games like Connect Four. By reducing the number of nodes that need to be evaluated, Alpha-Beta Pruning allows the AI to make deeper and more informed decisions within the same time frame. This approach is foundational for creating competitive AI in various strategic games.
Whether you’re developing AI for simple or complex games, mastering Minmax and Alpha-Beta Pruning will significantly enhance your AI’s performance, making it a formidable opponent in any game.
Stay tuned for more in-depth guides on AI algorithms and their practical applications in game development!
As Tech Co-Founder at Yugensys, I’m passionate about fostering innovation and propelling technological progress. By harnessing the power of cutting-edge solutions, I lead our team in delivering transformative IT services and Outsourced Product Development. My expertise lies in leveraging technology to empower businesses and ensure their success within the dynamic digital landscape.
Looking to augment your software engineering team with a team dedicated to impactful solutions and continuous advancement, feel free to connect with me. Yugensys can be your trusted partner in navigating the ever-evolving technological landscape.
Subscrible For Weekly Industry Updates and Yugensys Expert written Blogs
